Hệ tọa độ trong không gian là một công cụ quan trọng trong toán học và hình học, giúp xác định vị trí của các điểm trong không gian ba chiều. Đây là một khái niệm cơ bản được sử dụng rộng rãi trong nhiều lĩnh vực khoa học, kỹ thuật, và thậm chí trong đời sống hàng ngày. Việc hiểu và sử dụng hệ tọa độ trong không gian không chỉ giúp giải quyết các bài toán hình học mà còn đóng vai trò quan trọng trong việc mô phỏng, vẽ đồ thị, và tính toán trong nhiều lĩnh vực khác nhau.
Khái niệm về hệ tọa độ trong không gian
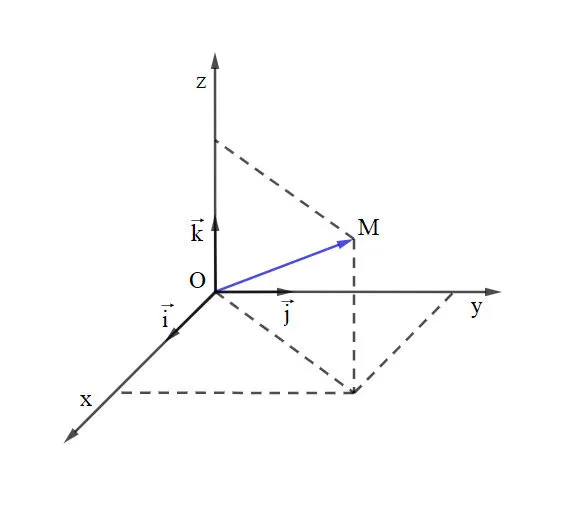
Hệ tọa độ trong không gian là một hệ thống dùng để xác định vị trí của các điểm trong không gian ba chiều, thường được biểu diễn bằng ba đại lượng độc lập. Trong không gian ba chiều, mỗi điểm sẽ được xác định bởi ba tọa độ, thường là (x, y, z), trong đó:
- x là khoảng cách của điểm đối với trục tọa độ x (trục hoành).
- y là khoảng cách của điểm đối với trục tọa độ y (trục tung).
- z là khoảng cách của điểm đối với trục tọa độ z (trục cao).

Những tọa độ này giúp xác định vị trí của điểm trong không gian ba chiều, từ đó có thể mô tả mọi đối tượng trong không gian.
Các hệ tọa độ phổ biến trong không gian
Trong không gian ba chiều, có nhiều loại hệ tọa độ trong không gian khác nhau, phổ biến nhất là hệ tọa độ Descartes (tọa độ vuông góc), hệ tọa độ cực và hệ tọa độ cầu.
-
Hệ tọa độ Descartes: Là hệ tọa độ mà các trục tọa độ x, y, và z vuông góc với nhau. Đây là hệ tọa độ phổ biến nhất và được sử dụng trong hầu hết các bài toán hình học không gian. Mỗi điểm trong không gian sẽ có ba tọa độ (x, y, z), tương ứng với các khoảng cách của điểm đó đối với ba trục.
-
Hệ tọa độ cực: Trong hệ tọa độ này, vị trí của điểm được xác định bởi khoảng cách từ gốc tọa độ và góc tạo bởi đoạn thẳng nối điểm với gốc tọa độ so với một trục cho trước. Hệ tọa độ này chủ yếu được sử dụng trong các bài toán liên quan đến hình học phẳng hoặc mô phỏng chuyển động theo vòng tròn.
-
Hệ tọa độ cầu: Được sử dụng để xác định vị trí của điểm trong không gian ba chiều bằng cách sử dụng ba thông số: bán kính, góc azimuthal (góc nằm ngang) và góc zenith (góc dọc). Hệ tọa độ cầu thường được áp dụng trong các bài toán vật lý, nhất là trong các nghiên cứu về thiên văn học và địa lý.
Các ứng dụng của hệ tọa độ trong không gian
Hệ tọa độ trong không gian có rất nhiều ứng dụng trong thực tiễn, từ các lĩnh vực khoa học cơ bản đến kỹ thuật và công nghệ.
-
Trong toán học: Hệ tọa độ trong không gian là công cụ cơ bản giúp giải quyết các bài toán hình học, đại số và phân tích. Các phép toán như phép cộng, phép trừ vector, độ dài đoạn thẳng, góc giữa các vector, hay các phép biến đổi không gian đều được thực hiện dễ dàng nhờ vào hệ tọa độ này.
-
Trong kỹ thuật: Các kỹ sư sử dụng hệ tọa độ trong không gian để mô phỏng, thiết kế các vật thể ba chiều, chẳng hạn như trong việc thiết kế máy móc, xây dựng kiến trúc, hoặc tạo mô hình 3D cho các sản phẩm công nghiệp. Việc ứng dụng hệ tọa độ trong không gian giúp việc lập bản vẽ, tính toán độ chính xác và mô phỏng sản phẩm trở nên đơn giản và hiệu quả hơn.
-
Trong khoa học tự nhiên: Hệ tọa độ trong không gian là công cụ không thể thiếu trong việc nghiên cứu các hiện tượng vật lý, như chuyển động của các thiên thể, vật thể trong không gian, hoặc các phép đo trong thí nghiệm vật lý. Ví dụ, trong lĩnh vực thiên văn học, các nhà khoa học sử dụng hệ tọa độ cầu để xác định vị trí của các ngôi sao, hành tinh và các vật thể vũ trụ khác.
-
Trong trò chơi điện tử và đồ họa máy tính: Các nhà phát triển game sử dụng hệ tọa độ trong không gian để tạo ra thế giới 3D trong các trò chơi điện tử. Bằng cách xác định vị trí của các đối tượng trong không gian 3D, các nhà phát triển có thể mô phỏng chuyển động và tạo ra hiệu ứng hình ảnh hấp dẫn.
Các phép toán với hệ tọa độ trong không gian
Khi làm việc với hệ tọa độ trong không gian, có một số phép toán cơ bản mà chúng ta thường xuyên sử dụng, chẳng hạn như:
- Cộng, trừ vector: Giúp xác định vị trí của các điểm mới trong không gian dựa trên các vector di chuyển.
- Tính khoảng cách giữa hai điểm: Đây là phép toán rất quan trọng, đặc biệt trong các bài toán hình học, khi cần xác định độ dài của đoạn thẳng nối hai điểm trong không gian.
- Tính góc giữa các vector: Giúp xác định mối quan hệ hướng giữa các vector trong không gian, điều này có ý nghĩa quan trọng trong các bài toán vật lý.
Toán Hình học 12 Hệ tọa độ trong không gian | Hoc247
Cảm ơn các em đã xem Video hướng dẫn giải BT Hình học 12 Chương 3 Bài 1 của Thầy Lê Minh Thuận về Hệ tọa độ trong không gian.
👉 Đăng ký Học MIỄN PHÍ tại
👉 LIKE và SHARE các bài giảng để bạn bè cùng vào học tập nhé!
——- Theo dõi HỌC247 trên MXH ——-
+ Facebook:
+ Youtube:
+ Website học tập:hoc247.vn và hoc247.net
— Xem video khác —
-Giải bài tập SGK Toán 12 – Thầy Lê Minh Thuận | HỌC247
-Luyện thi THPT QG môn Toán – TS Phạm Sỹ Nam | HỌC247
Mong được đồng hành cùng các em học sinh
Trân trọng !
—————————————-
© Copyright by HỌC247 THPT ❌ Do not Reup ❌
Nguồn: https://paranormal-association.com/
Xem thêm bài viết khác:
Ôn tập học kì 1 Toán 11: Phần 1 Đại số và Giải tích | HỌC247